模式识别 U4 Fisher线性判别

Fisher Discriminant

4.1 Fisher线性判别动机
4.2 Fisher线性判别分析
4.3 Fisher线性判别算法

课程内容

Fisher线性判别动机

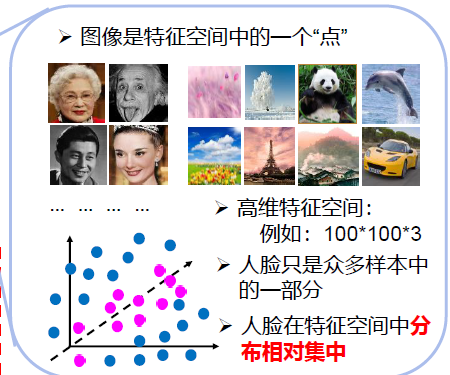
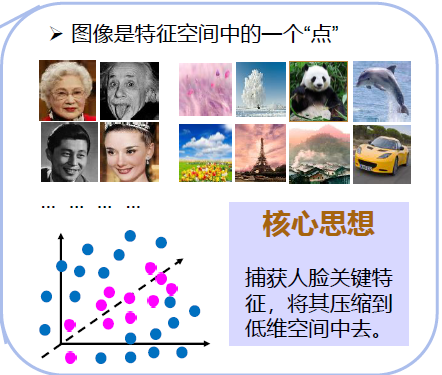
Fisher判别的核心思想是：在两个类别之间找到最好的区分，进行特征降维

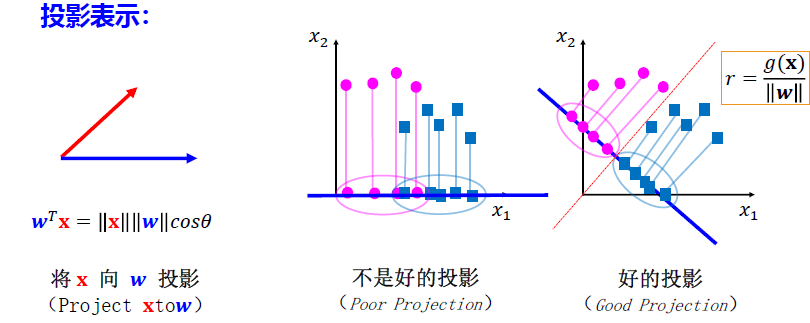
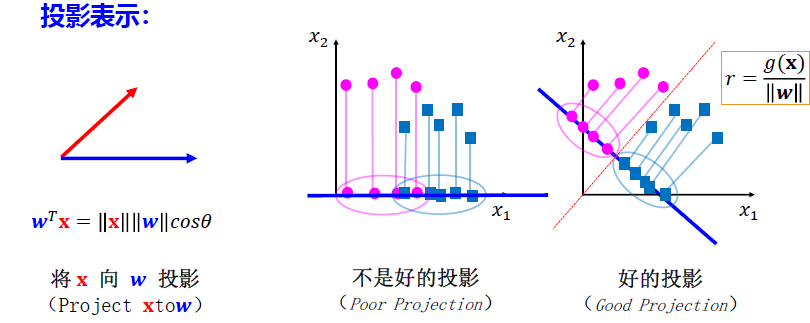
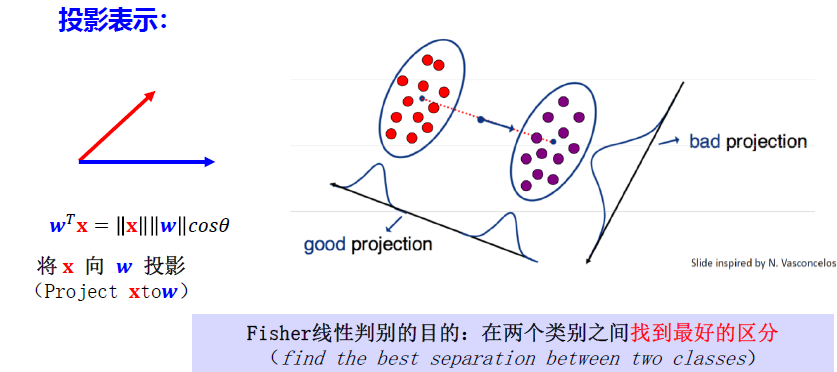
Fisher判别目的

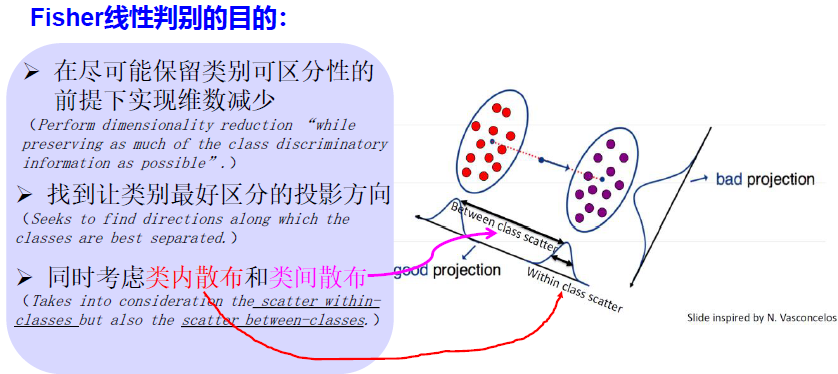
Fisher线性判别分析

线性回归目的：找到误差最小的拟合模型

二分类问题的Fisher线性判别：学习最佳投影，它能将所有样本投影到w的方向

目标函数

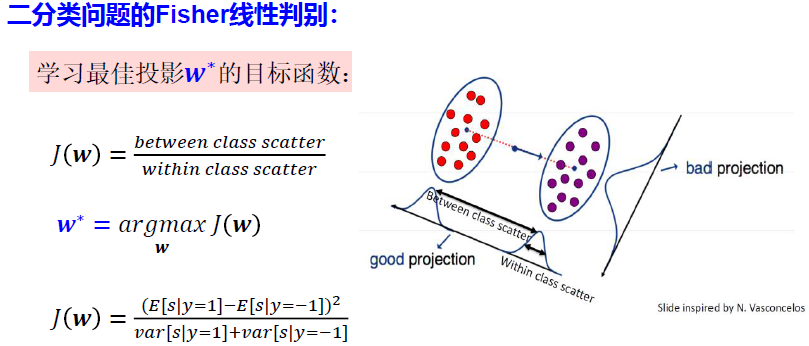
代数推演过程

目标函数 \[ \begin{align*} J(\mathbf w)&=\frac{类间差异}{类内差异}\\ \mathbf{w}^* &= \arg \mathop{\max}\limits_{\mathbf w}J(\mathbf w)\\ \end{align*} \] 在上述二分类问题中，则有 \[ J(\mathbf w)=\frac{(\mathbb E[s|y=1]-\mathbb E[s|y=-1])^2}{var[s|y=1]+var[s|y=-1]} \] 对分子： $$ (E[s|y=1]-)^2\ \[\begin{align*} &=(\mathbb E[\mathbf w^T\mathbf x|y=1]-\mathbb E[\mathbf w^T\mathbf x|y=-1])^2\\ &=\Big(\mathbf w^T(\mathbb E[\mathbf x|y=1]-\mathbb E[\mathbf x|y=-1])\Big)^2\\ \end{align*}\] $$ 根据概率论知识，$\mathbb E[\mathbf x|y=c]=\frac{1}{N}\sum_{i=1}^{N_c}[x_i|y=c]=\mu_c$

因而我们可以改写上式： $$ (E[s|y=1]-)^2\ \[\begin{align*} &=\Big(\mathbf w^T(\mathbb E[\mathbf x|y=1]-\mathbb E[\mathbf x|y=-1])\Big)^2\\ &=\Big(\mathbf w^T(\mu_1-\mu_{-1})\Big)^2\\ &=\mathbf w^T(\mu_1-\mu_{-1})(\mu_1-\mu_{-1})^T\mathbf w \end{align*}\] $$ 对分母：

根据协方差计算方法：$var[s|y=c]=\mathbb E[(s-\mathbb E[s|y=c])^2]$

则有： \[ \begin{align*} var[s|y=c]&=\mathbb E[(s-\mathbb E[s|y=c])^2]\\ \\ &=\mathbb E[(\mathbf w^T\mathbf x-\mathbb E[\mathbf w^T\mathbf x|y=c])^2]\\ \\ &=\mathbb E[\Big(\mathbf w^T(\mathbf x-\mathbb E[\mathbf x|y=c])\Big)^2]\\ \\ &=\mathbb E[\Big(\mathbf w^T(\mathbf x-\mu_c)\Big)^2]\\ \\ &=\mathbb E[\mathbf w^T(\mathbf x-\mu_c)(\mathbf x-\mu_c)^T \mathbf w]\\ \\ &=\mathbf w^T\mathbb E[(\mathbf x-\mu_c)(\mathbf x-\mu_c)^T]\mathbf w\\ \\ &=\mathbf w^T\mathbb \Sigma_c\mathbf w\\ \end{align*} \] 因此： \[ var[s|y=c]=\mathbf w^T\mathbb \Sigma_c\mathbf w\\ \Sigma_c=\frac{1}{N_C}\sum^{Nc}_{n=1}[(\mathbf x_n-\mu_c)(\mathbf x_n-\mu_c)^T|y=c] \] 综上：

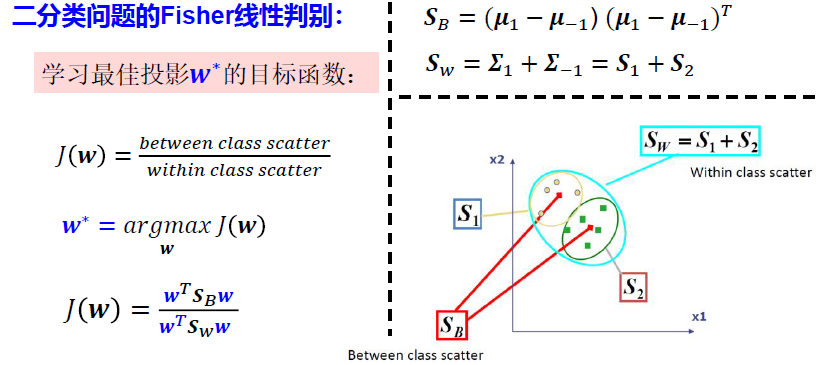
优化问题：线性规划+拉格朗日乘数法

$$ \[\begin{align*} J(\mathbf w)&=\frac{(\mathbb E[s|y=1]-\mathbb E[s|y=-1])^2}{var[s|y=1]+var[s|y=-1]}\\ &=\frac{\mathbf w^TS_{B(between)}\mathbf w}{\mathbf w^TS_{W(within)}\mathbf w}\\ \\ \mathbf{w}^* &= \arg \mathop{\max}\limits_{\mathbf w}J(\mathbf w)\\ \end{align*}\] $$

分式的最优化不好处理，我们利用拉格朗日乘数法将其转化为易处理的形式

我们假定分母一定，此时取得分子的最大值，即可最大化目标函数

用数学语言表示为↓ \[ \arg \max_{\mathbf w}\space\space (\mathbf w^TS_{B}\mathbf w) \space\space Subject \space to\space\space(\mathbf w^TS_{W}\mathbf w=K) \] $Lagrange\space Multipliers:$ $$ \[\begin{align*} L(\mathbf w, \lambda)&=\mathbf w^TS_{B}\mathbf w+\lambda(K-\mathbf w^TS_{W}\mathbf w)\\ &=\mathbf w^T(S_{B}-\lambda S_{W})\mathbf w + \lambda K\\ \\ 令： \nabla L_{\mathbf w}(\mathbf w, \lambda)&=\frac{\partial L(\mathbf w, \lambda)}{\part \mathbf w}=2(S_{B}-\lambda S_{W})\mathbf w=\mathbf 0^T\\ 则：S_{B}\mathbf w&=\lambda S_{W}\mathbf w \end{align*}\] $$