PatternRecognition-5-Logistic回归
模式识别 U5 Logistic 回归
课堂内容
- 5.1 Logistic回归问题
- 5.2 Logistic回归损失
- 5.3 Logistic回归算法
- 5.4 二元分类线性模型讨论
5.1 逻辑斯蒂回归问题
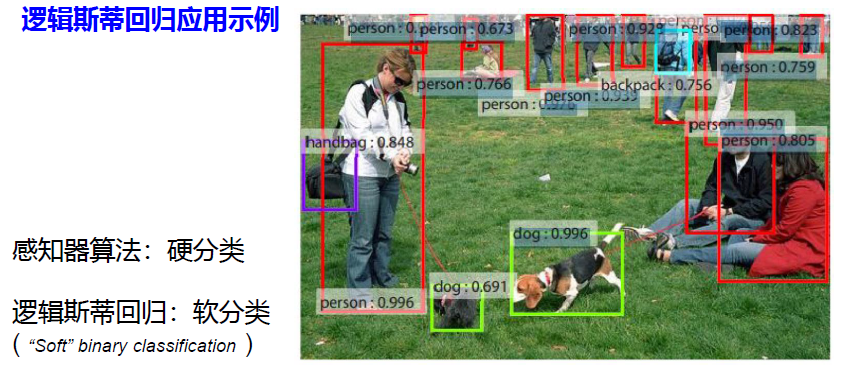
逻辑斯蒂回归是一种“软分类”策略,即考虑分类中的概率性或称模糊性
逻辑回归假设数据服从伯努利分布,通过极大似然函数的方法,运用梯度下降来求解参数,来达到将数据二分类的目的


5.2 逻辑斯蒂回归损失
往期损失函数回顾
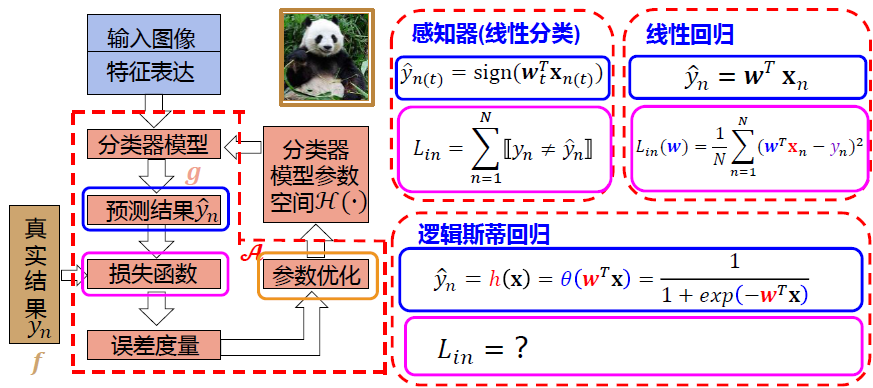
逻辑斯蒂回归可以使用平方损失函数作为损失函数吗?
平方损失
数学推演: \[ h(\mathbf x)=\theta(\mathbf w^T\mathbf x)=\frac{1}{1+e^{-\mathbf w^T\mathbf x}}\\ \\ \mathcal L_{in}(\mathbf w)=(\theta(\mathbf w^T\mathbf x)-y)^2\\ \] 存在一个问题:

由实际训练样本标签带来的影响,我们改写损失函数形式为: \[ \mathcal L_{in}(\mathbf w)=(\theta(y\mathbf w^T\mathbf x)-1)^2\\ \] 由此进行梯度推演:
$$ \[\begin{align*} \frac{\partial \mathcal L_{in}(\mathbf w,\mathbf x,y)}{\partial w_i}&=2[\theta(y\mathbf w^T\mathbf x)-1]\frac{\partial\theta(\mathbf w)}{\partial w_i}\\ &=2[\theta(y\mathbf w^T\mathbf x)-1]\frac{yx_ie^{-y\mathbf w^T\mathbf x}}{(1+e^{-y\mathbf w^T\mathbf x})^2}\\ &=2[\theta(y\mathbf w^T\mathbf x)-1]yx_i\frac{1}{(1+e^{-y\mathbf w^T\mathbf x})}\frac{e^{-y\mathbf w^T\mathbf x}}{(1+e^{-y\mathbf w^T\mathbf x})}\\ &=2[\theta(y\mathbf w^T\mathbf x)-1]yx_i\theta(y\mathbf w^T\mathbf x)[1-\theta(y\mathbf w^T\mathbf x)]\\ \theta&(y\mathbf w^T\mathbf x)\gt0 (正确分类)\space \space \nabla\mathcal L \rightarrow 0\\ \theta&(y\mathbf w^T\mathbf x)\lt0(错误分类)\space \space \nabla\mathcal L \rightarrow 0\\ \end{align*}\]\ $$

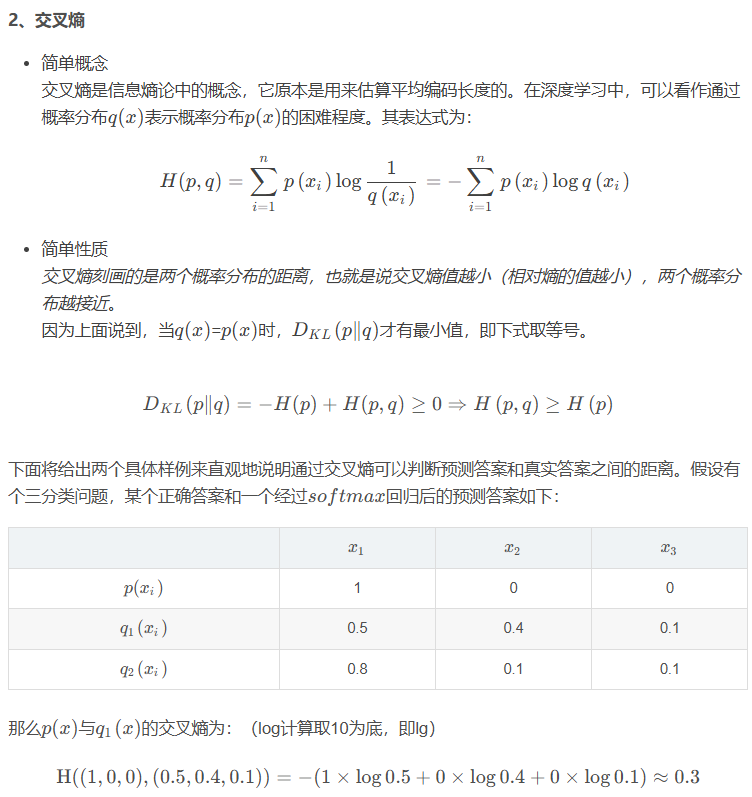
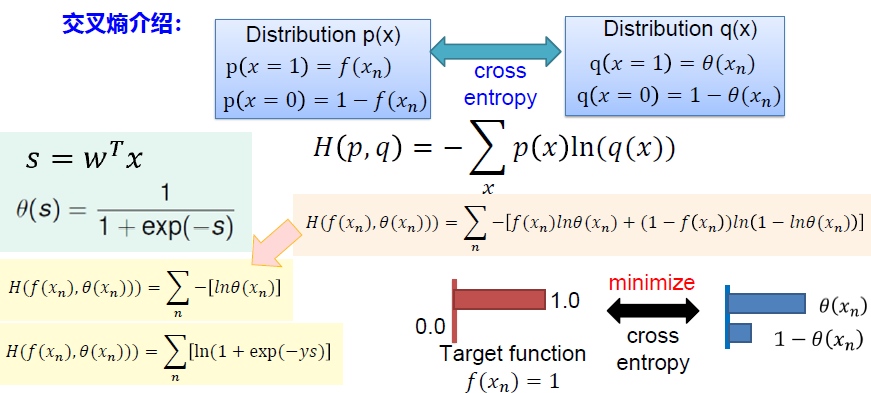
交叉熵损失

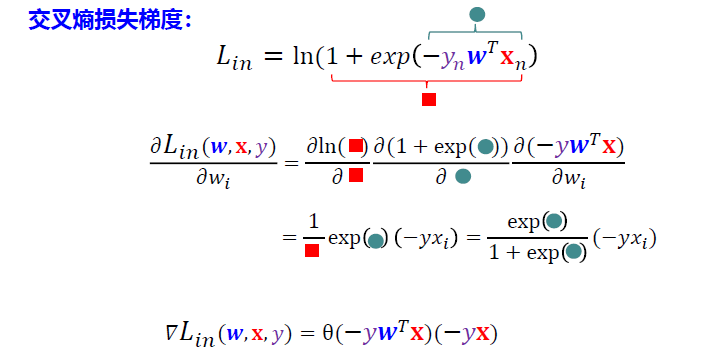
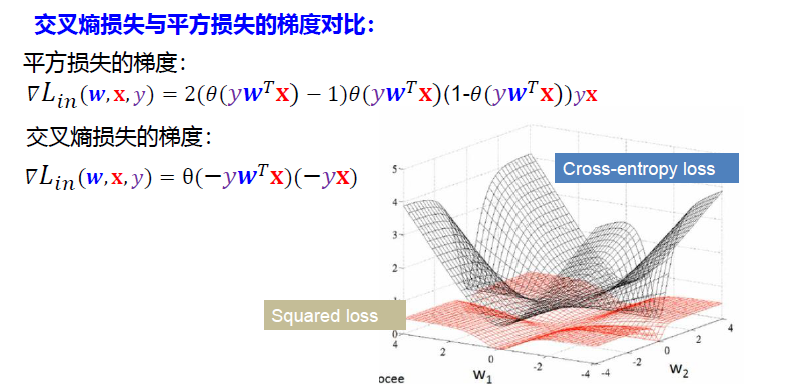
5.3 逻辑斯蒂回归算法



5.4 二元分类线性模型讨论
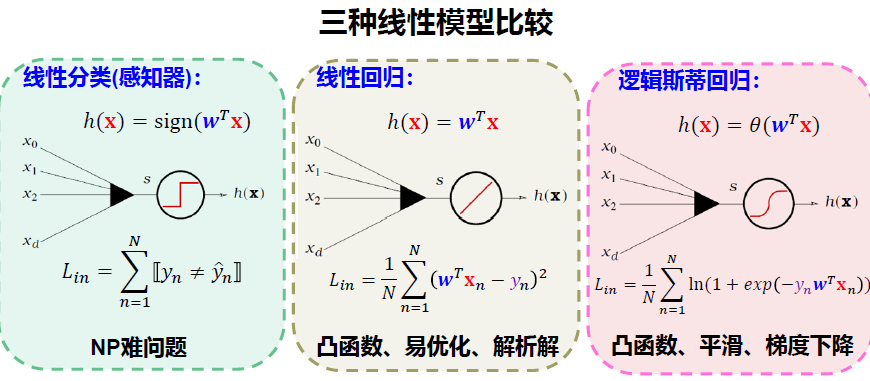

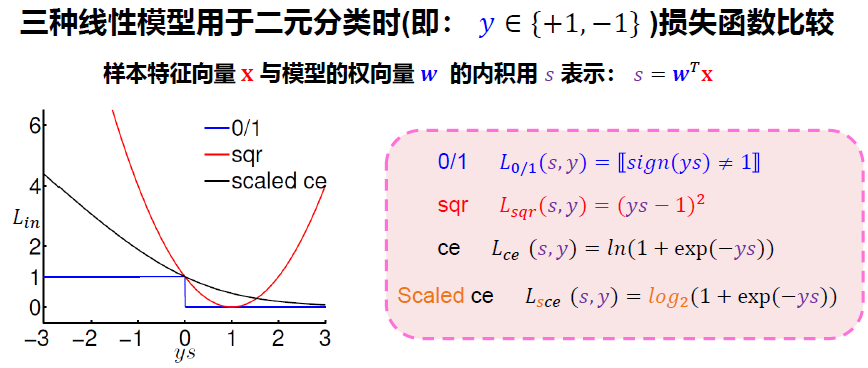


小结