PatternRecognition-6-SVM
模式识别 U5 支撑向量机 SVM
- 第五次课 – 非线性分类
- 第六次课 – 线性支撑向量机
- 第七次课 – 对偶与核支撑向量机
课堂内容
U5 - 1 非线性变换
- 1 线性不可分问题
- 2 非线性变换
- 3 知识扩展
1.线性不可分问题
先前学习PLA感知机时,PLA可以收敛的必要条件是 数据集线性可分
在面对线性不可分问题时,所有的线性模型,如PLA,Pocket,LinearRegression, Fisher, LogisticRecognition 均只能在一定的误差范围内取得最优(通过梯度下降或者0-1权重迭代)
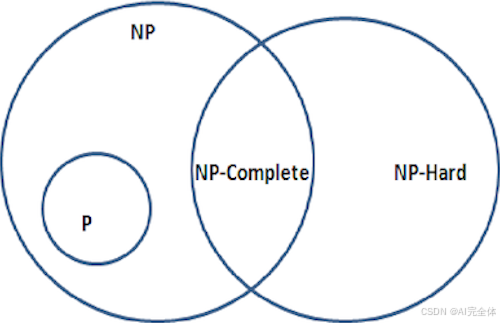
对于线性模型,线性不可分的数据集的求解变成一个 NP难问题
如何突破线性分类限制,成为我们本章讨论的重点
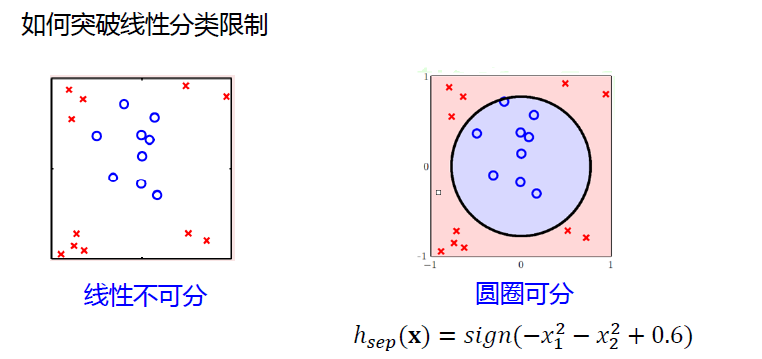
扩展思维,将原有的线性模型\(\mathbf w^T\mathbf x\)一阶线性公式升维为高阶

引入概念:核函数 \(\Phi\)
核函数解决线性不可分的本质思想就是把原始的样本通过核函数映射到高维空间中,让样本在高维特征空间中是线性可分的,然后再使用常见的线性分类器,如SVM就可以很好的分类了。
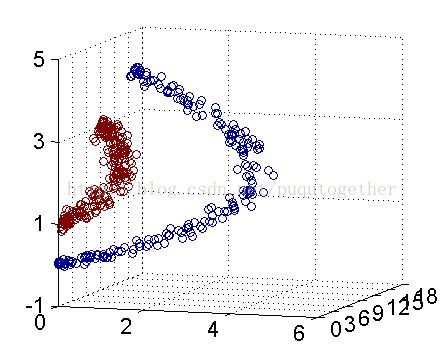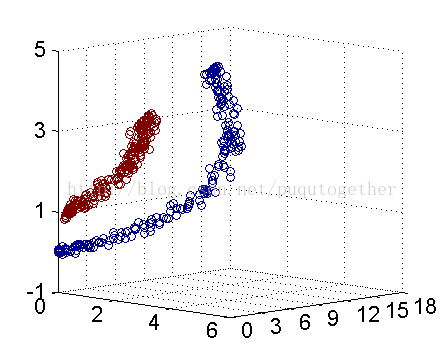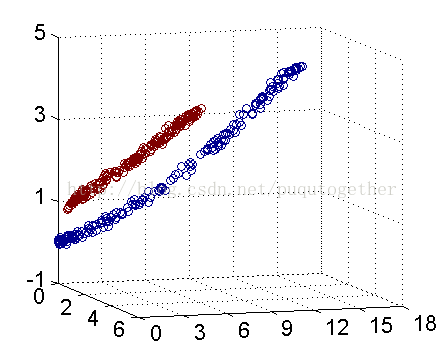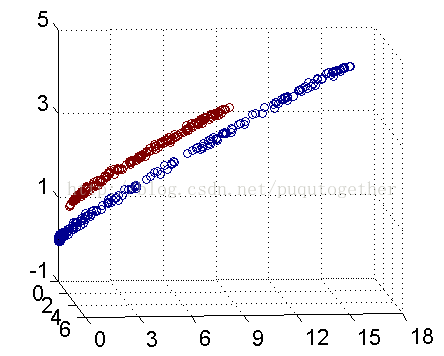
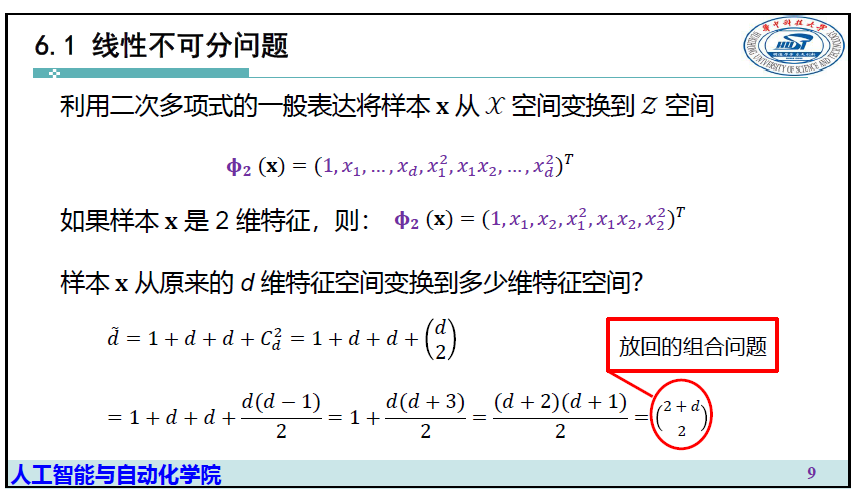
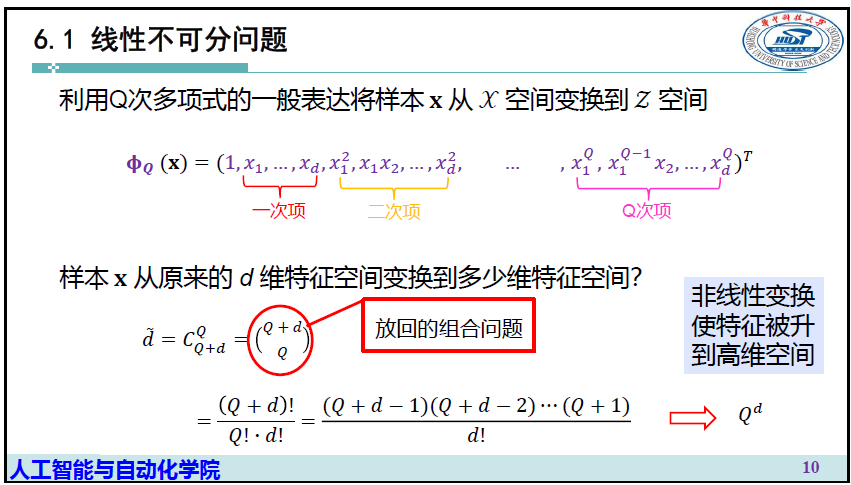
2.非线性变换
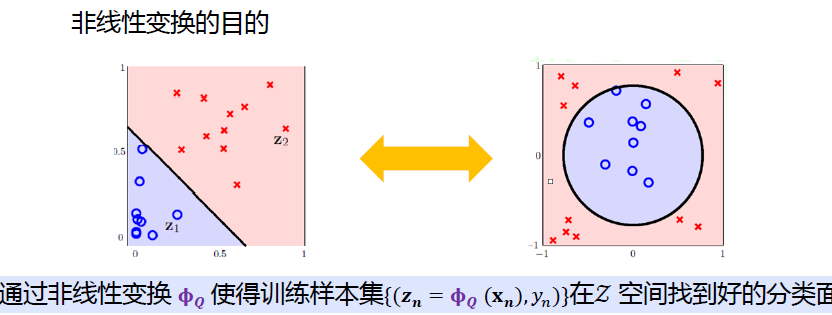
使得训练集在高维空间中找到更好的分类面
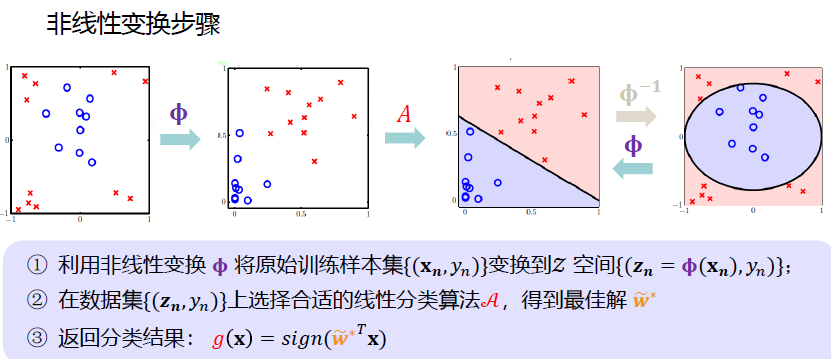
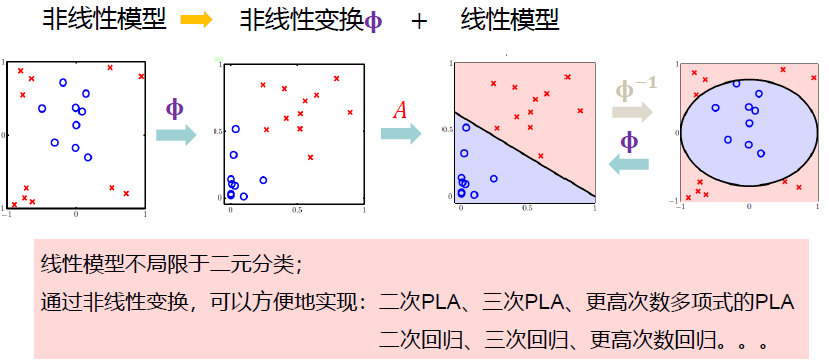

3.知识扩展:模型泛化能力的讨论


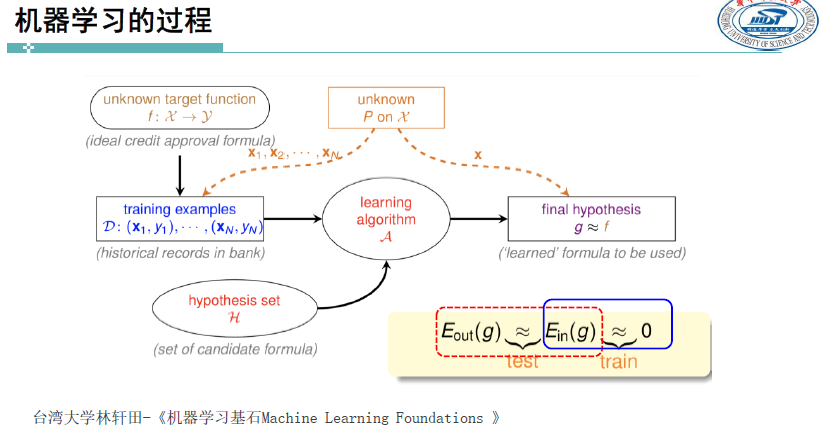

霍夫丁不等式:给出了随机变量的和与其期望值偏差的概率上限
$$ Hoffding's Inequality:\
P[|v-|>] 2e{-22N} $$ 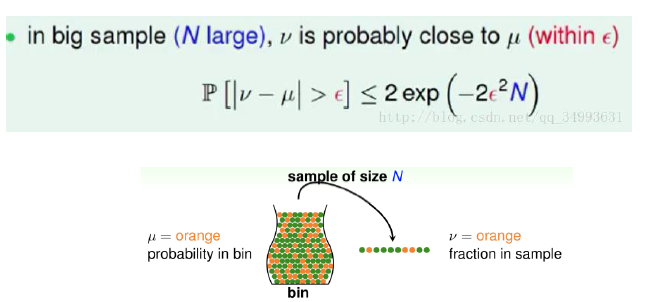
VC 维 VC Bound

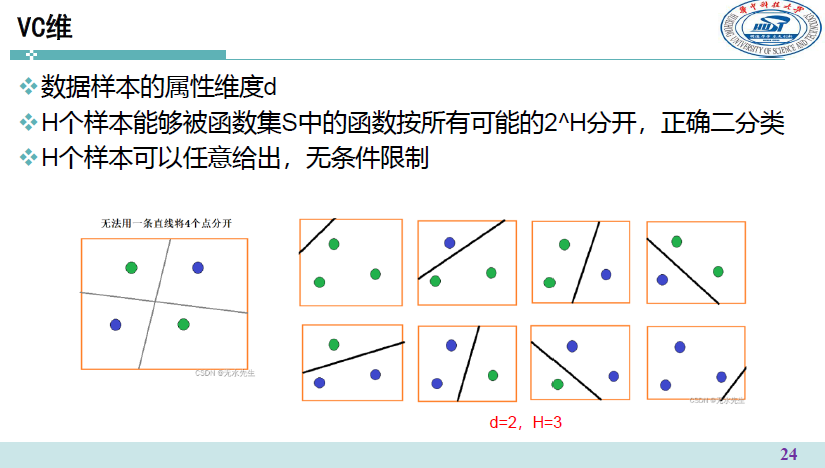

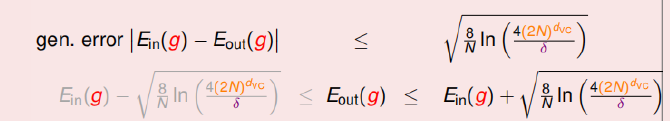


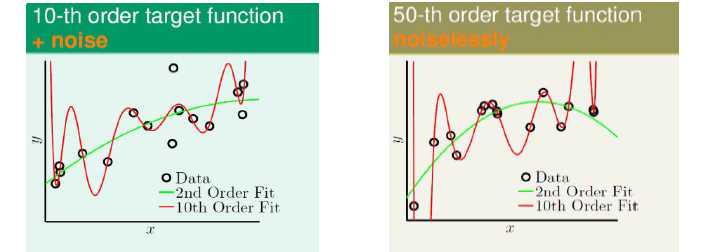
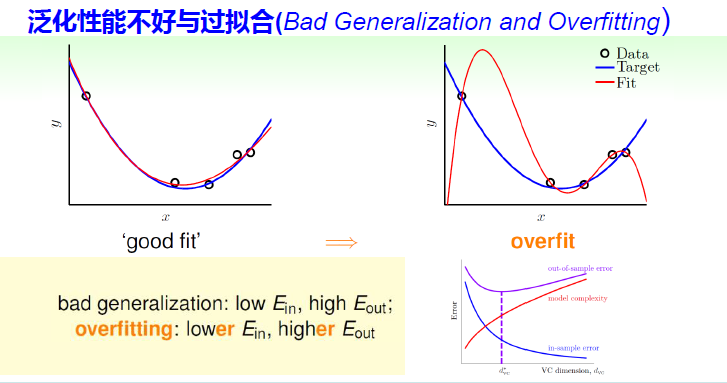
由上述分析知,想要在训练集上得到更低的训练误差,模型的复杂度就会上升。由于泛化误差上界受训练误差和模型复杂度共同的影响,所以并非一味降低训练误差就可以得到更好的泛化结果
过拟合问题
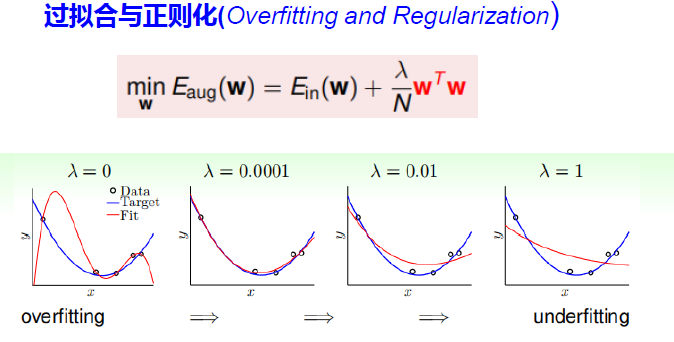
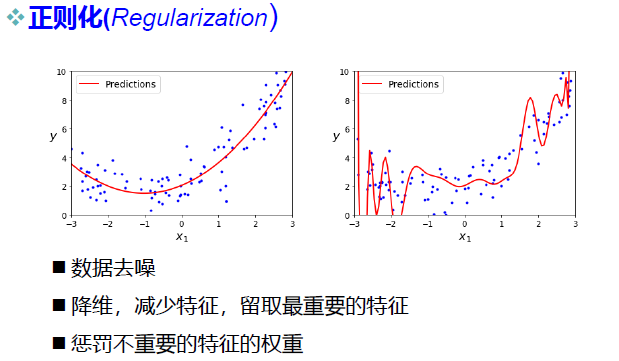
补充:正则化问题
- 什么是正则化(Regularization)?
- 正则化是一种常用的技术,用于控制模型的复杂度,减少过拟合的风险。它通过在损失函数中引入额外的项来对模型的参数进行约束或惩罚,使模型更加简单、平滑或稀疏。
- 正则化是用来防止模型过拟合而采取的手段
总结一下:
欠拟合:泛化能力差,训练样本集准确率低,测试样本集准确率低。 过拟合:泛化能力差,训练样本集准确率高,测试样本集准确率低。 合适的拟合程度:泛化能力强,训练样本集准确率高,测试样本集准确率高
- 欠拟合原因:
- 训练样本数量少 模型复杂度过低 参数还未收敛就停止循环
- 欠拟合的解决办法:
- 增加样本数量 增加模型参数,提高模型复杂度 增加循环次数 查看是否是学习率过高导致模型无法收敛
- 过拟合原因:
- 数据噪声太大 特征太多 模型太复杂
- 过拟合的解决办法:
- 清洗数据 减少模型参数,降低模型复杂度 增加惩罚因子(正则化),保留所有的特征,但是减少参数的大小(magnitude)。
小结

U5 - 2 线性支撑向量机
- 7.1 最大间隔分类面
- 7.2 标准的最大间隔问题
- 7.3 支撑向量机 SVM (Support Vector Machine)
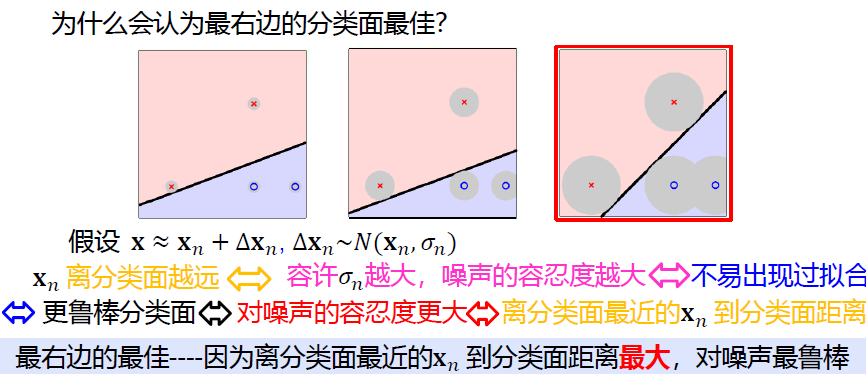
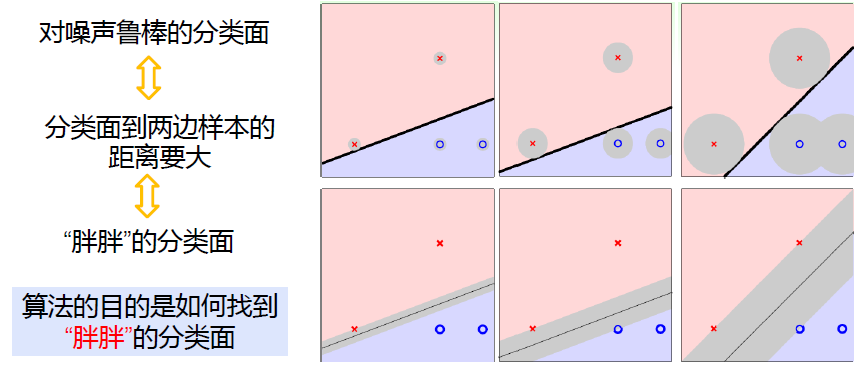
1 最大间隔分类面
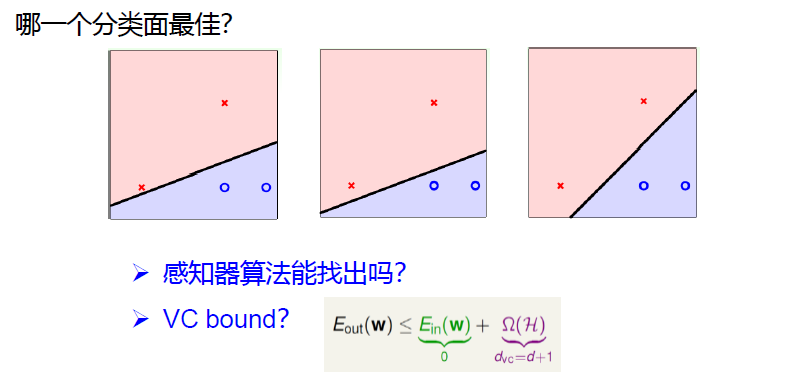
2 标准的最大间隔问题
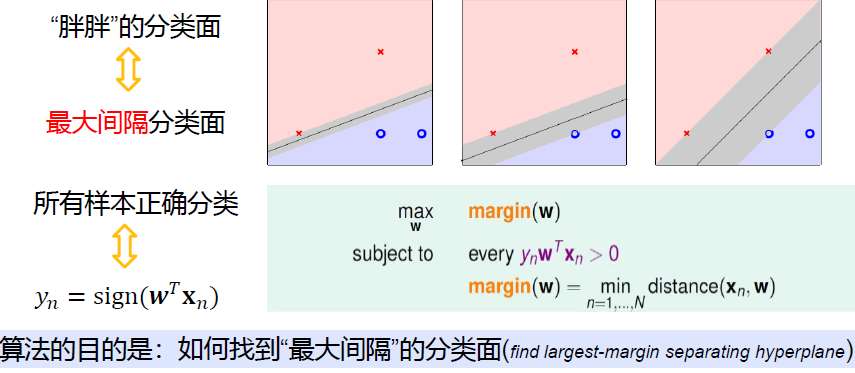
对“寻找最大间隔”进行数学语言上的定义


回到了U2讨论距离的公式
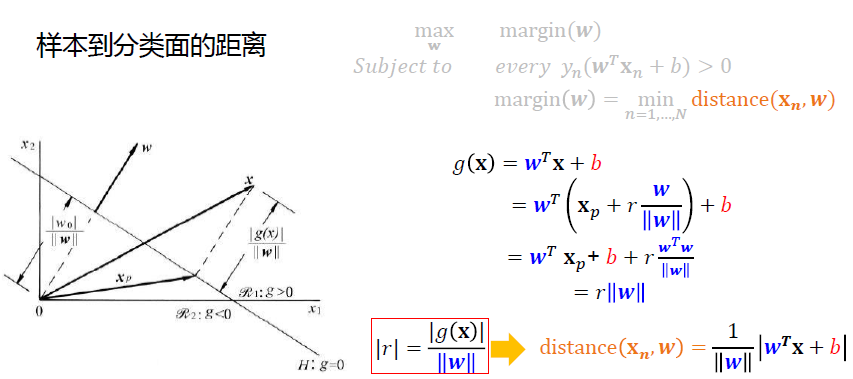

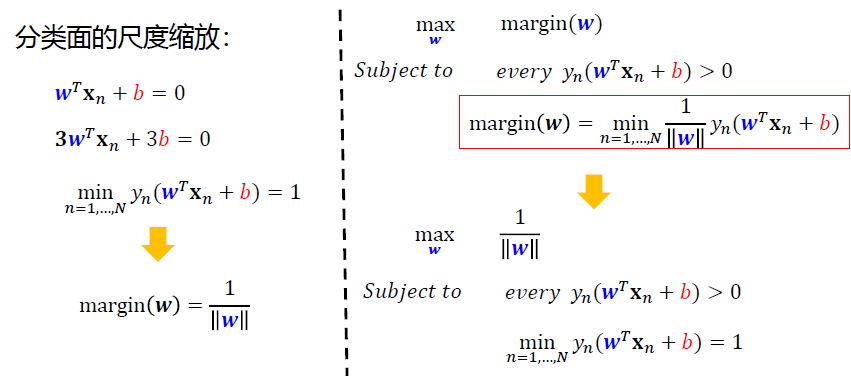

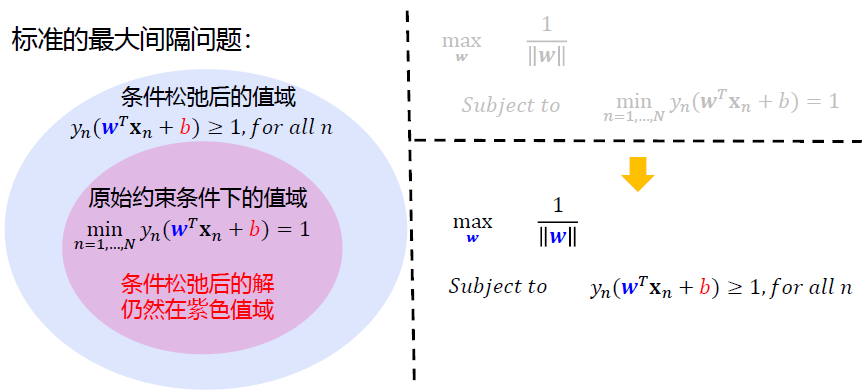



经过一系列数学推导,原最大间隔问题: \[ \begin{align*} &\max_{\mathbf w}\space\space margin(\mathbf w)=\min_{n=1,...,N}\frac{y_n(\mathbf w^T\mathbf x_n+b)}{||\mathbf w||}\\ &Subject \space to\space\space every\space y_n(\mathbf w^T\mathbf x_n+b)\ge0 \end{align*} \] 通过一系列变换: \[ \begin{align*} \min_{n=1,...,N}y_n(\mathbf w&^T \mathbf x_n +b)=1\\ &↓\\ \max_{\mathbf w}\space\space margin&(\mathbf w)=\frac{1}{||\mathbf w||}\\ &↓\\ \min_{\mathbf w}\space &||\mathbf w||\\ &↓\\ \min_{\mathbf w}\space &\frac{1}{2}\mathbf w^T\mathbf w\\ \end{align*} \]
变为了最终: \[ \begin{align*} &\min_{\mathbf w}\space \frac{1}{2}\mathbf w^T\mathbf w\\ subject\space to \space \space &y_n(\mathbf w^T\mathbf x_n+b)\ge1,for \space all\space n \end{align*} \]
3 支撑向量机 Support Vector Machine
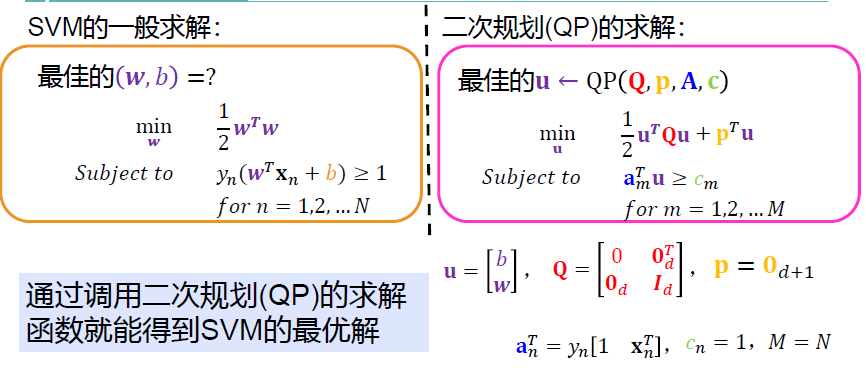
SVM建模 算法分析
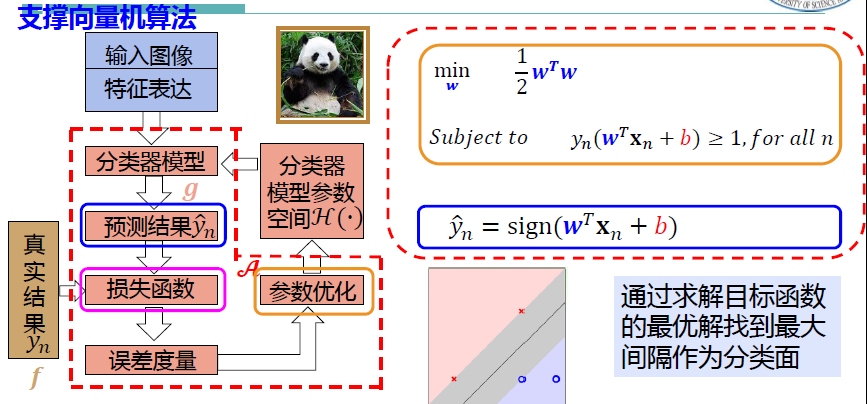


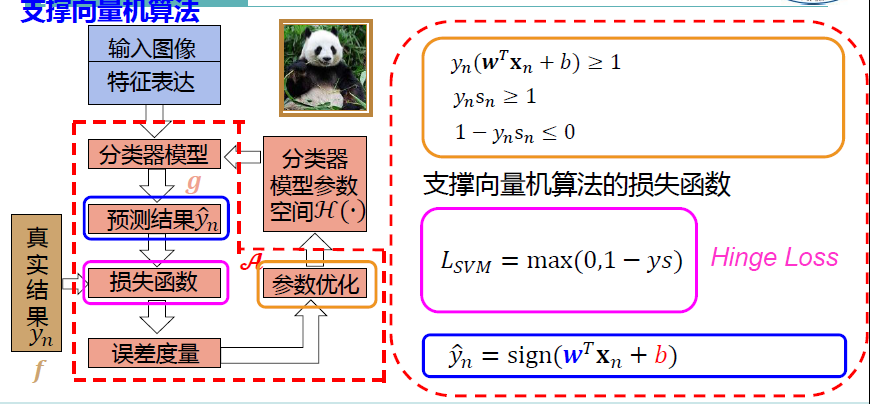


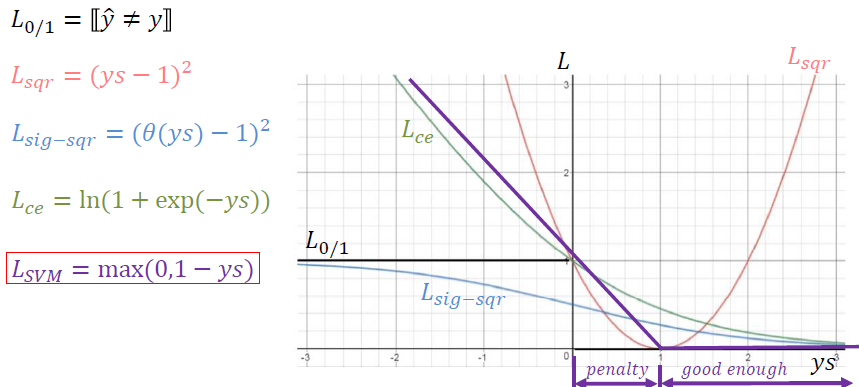
因为SVM的标准数学描述中含有约束条件,梯度下降难以寻找到一个下降的最优方向
然而这个问题是个凸函数,可以用凸二次规划的方法来求解
二次规划(QP)的求解




小结
U5 - 3 对偶支撑向量机和核支撑向量机
Dual SVM & Kernel SVM
- 8.1 对偶支撑向量机 动机
- 8.2 对偶支撑向量机的拉格朗日分析
- 8.3 求解对偶支撑向量机最佳值
- 8.4 对偶支撑向量机讨论
- 8.5 核函数支撑向量机
1 对偶支撑向量机动机
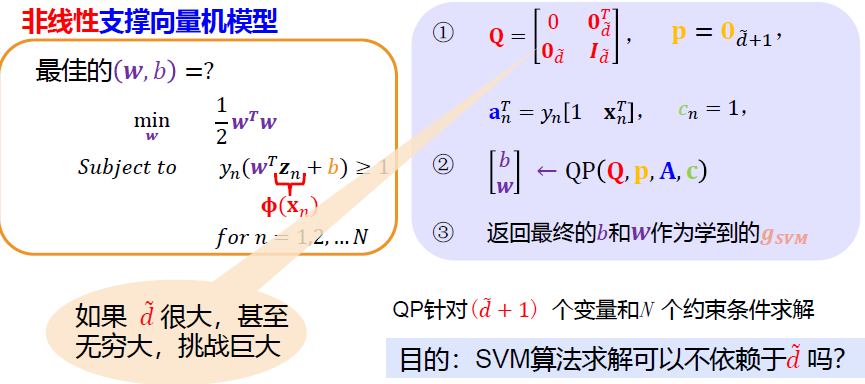

以下引用周志华老师《机器学习》中的内容:
我们希望求解下式来得到大间隔划分超平面所对应的模型 \[ \begin{align*} &\min_{\mathbf w}\space \frac{1}{2}\mathbf w^T\mathbf w\\ subject\space to \space \space &y_n(\mathbf w^T\mathbf x_n+b)\ge1,for \space all\space n \end{align*} \]
\[ g(\mathbf x)=\mathbf w^T\mathbf x+b \]
其中\(\mathbf w\)和\(b\)是模型参数
注意到,上式本身是一个凸二次规划(convex quadratic programming)问题,可以直接用QP优化计算包求解,但我们可以考虑一种更高效的方法
对其使用Lagrange乘子法可得到其“对偶问题Dual”
具体来说,对上式的每条约束添加拉格朗日乘子\(\alpha_i \ge 0\),则上式可改写: \[ \begin{align*} L(\mathbf w,b, \pmb{\alpha})=\frac{1}{2}||\mathbf w||^2+\sum^m_{i=1}\alpha_i(1-y_i(\mathbf w^T\mathbf x_i+b)) \end{align*} \] 其中\(\pmb \alpha=[\alpha_1;\alpha_2;...;\alpha_m]\)
\(L(\mathbf w,b, \pmb{\alpha})\)对\(\mathbf w\)和b求偏导: \[ \frac{\partial L(\mathbf w,b, \pmb{\alpha})}{\partial \mathbf w}=\mathbf w-\sum^m_{i=1}\alpha_iy_i\mathbf x_i=0\\ \frac{\partial L(\mathbf w,b, \pmb{\alpha})}{\partial b}=-\sum^m_{i=1}\alpha_iy_i=0\\ \] 由此知 \[ \mathbf w=\sum^m_{i=1}\alpha_iy_i\mathbf x_i\\ 0=\sum^m_{i=1}\alpha_iy_i \] 于是我们得到了SVM的Dual形式↓ \[ \begin{align*} &\max_{\pmb \alpha}\space \sum_{i=1}^m\alpha_i-\frac{1}{2}\sum_{i=1}^m\sum_{j=1}^m\alpha_i\alpha_jy_iy_j\mathbf x_i^T\mathbf x_j\\ &s.t. \space\space\space \sum_{i=1}^m\alpha_iy_i=0 \end{align*} \] 解出\(\alpha\)后求出w和b即可
因为用了拉格朗日乘子法,故还需要满足KKT条件 \[ KKT: \begin{cases} \alpha_i \ge 0;\\ y_if(\mathbf x_i)-1 \ge 0;\\ \alpha_i(y_if(\mathbf x_i)-1)=0. \end{cases} \]
2 对偶支撑向量机的拉格朗日分析


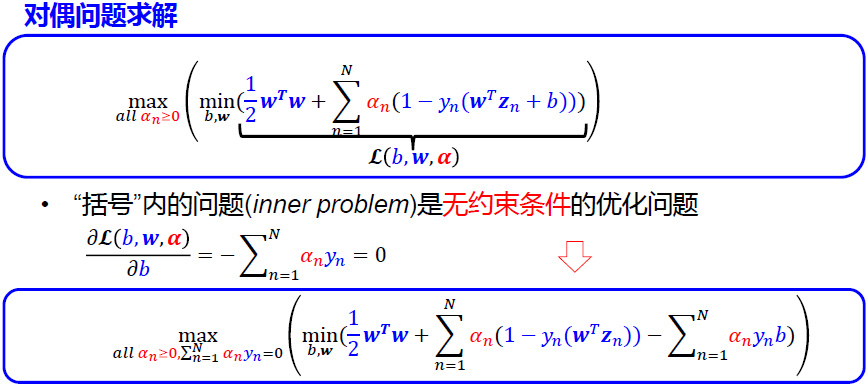
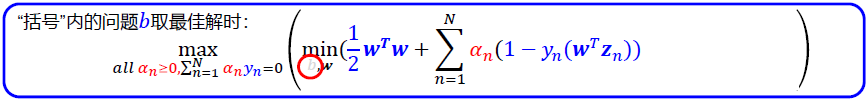
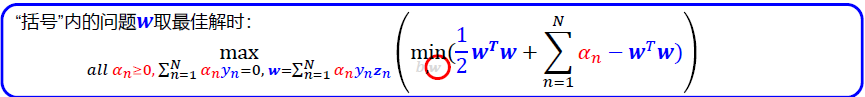



3 求解对偶支撑向量机最佳值
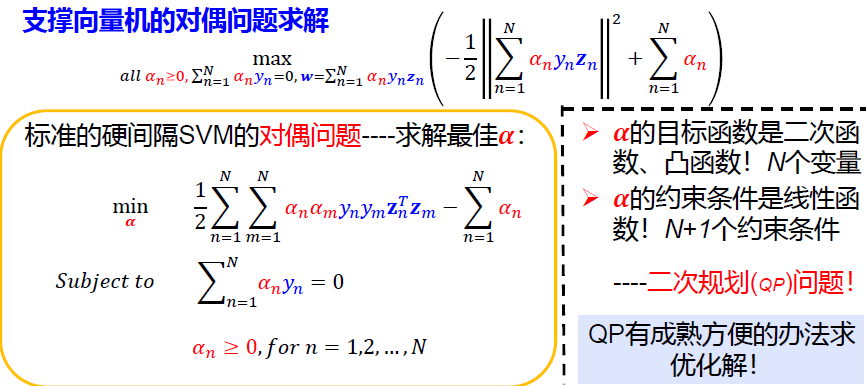



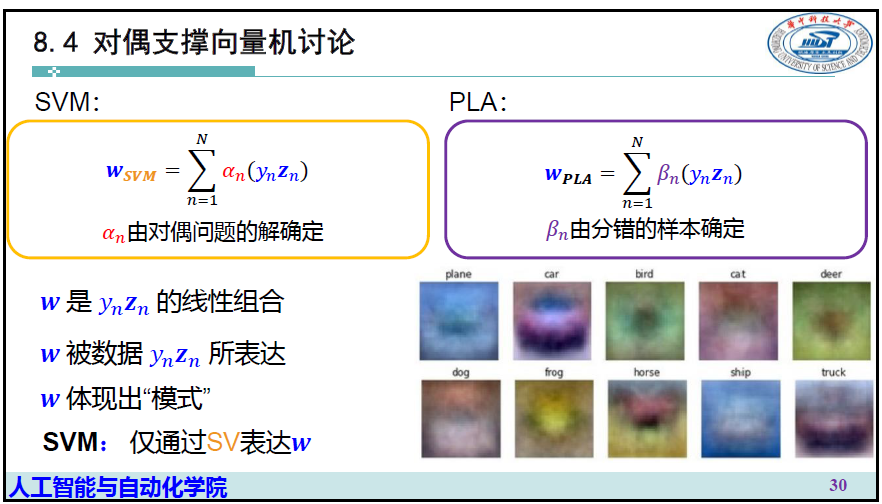
4 对偶支撑向量机的讨论


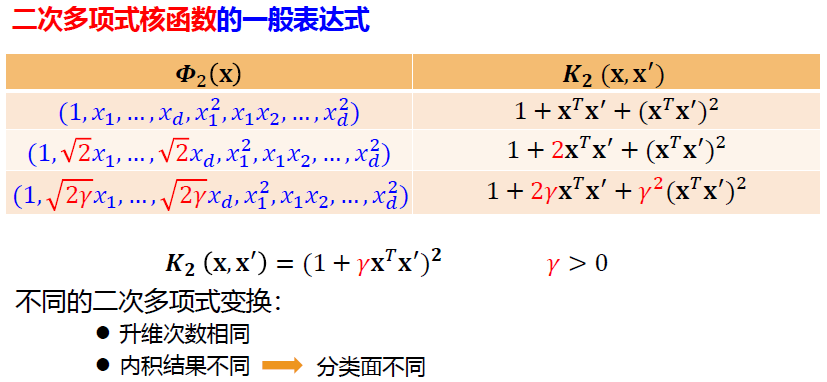
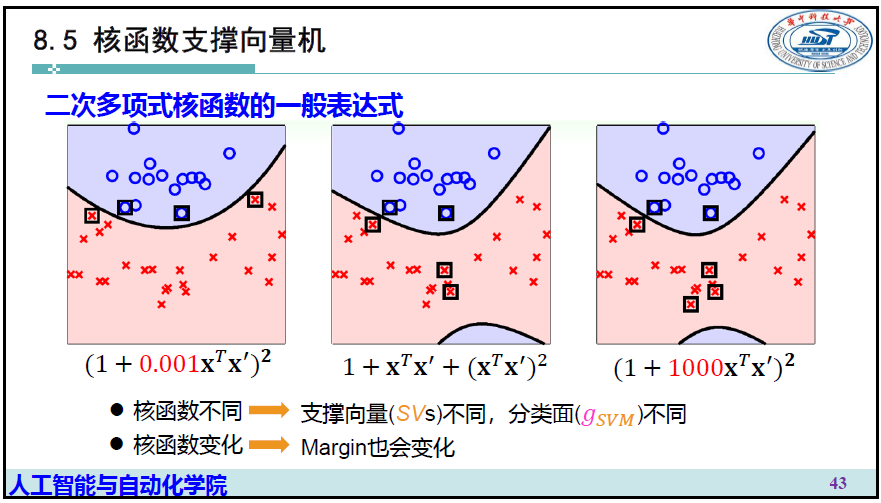
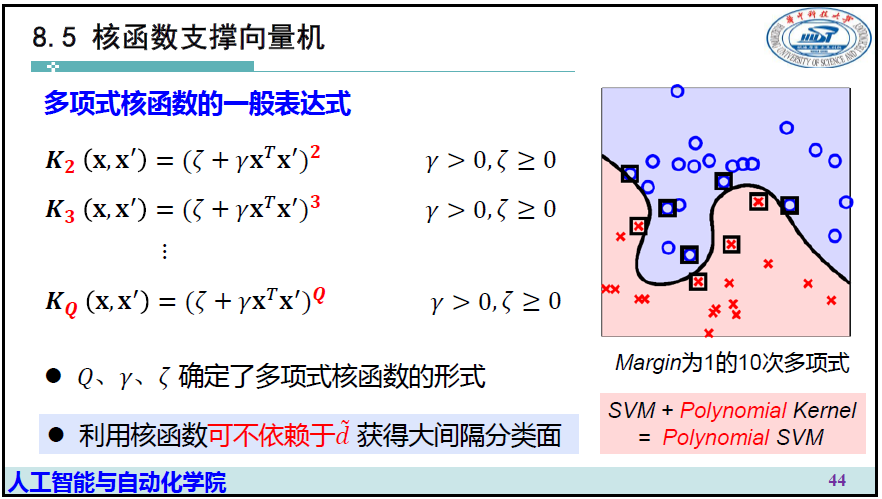
5 核函数支撑向量机








小结







