模式识别 U3 线性回归 Linear Regression

课程内容

  • 3.1 线性回归问题
  • 3.2 线性回归算法
  • 3.3 梯度下降法

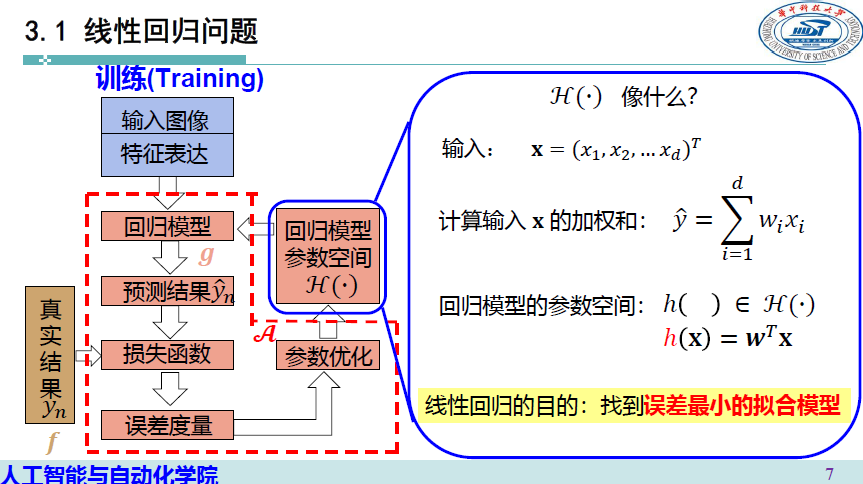
线性回归问题

机器学习的过程其实是一个找最拟合函数的过程，通过不断的训练，我们最终得到一个函数映射，给定函数（网络）一个输入，函数（网络）会给出相应的输出

若输出的是一个数值（scatter），我们就将这类机器学习问题称为回归Regression

线性回归算法

模型构建

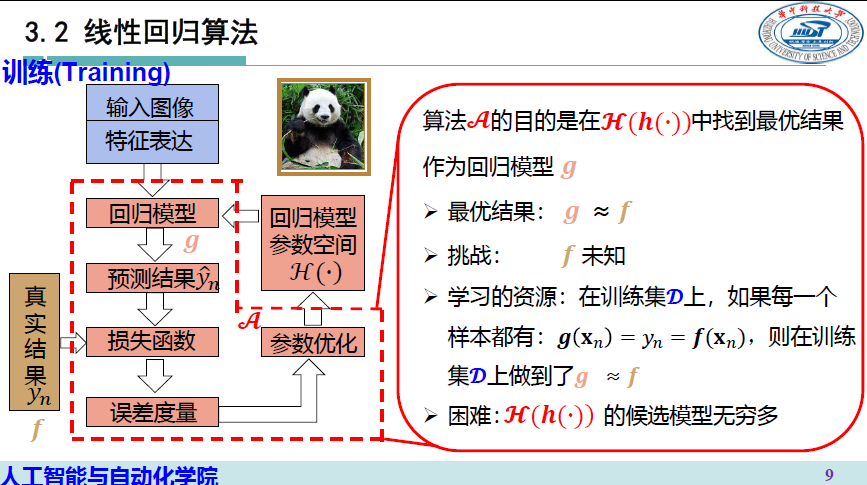
为达到回归目的，我们度量模型输出结果时不再仅仅关注输出的符号

而是关注模型输出的数值

由此，我们择取 “平方误差函数”作为我们的损失函数，来度量我们的模型学习效果 \[ \begin{align*} \mathcal{L}&=(\hat{y_n}-y_n)^2 \\ \mathcal{L_{in}}&=\frac{1}{N}\sum^N_{n=1}(\hat{y_n}-y_n)^2 \end{align*} \] \(\mathcal{L}_{in}\)计算训练样本集所有样本产生的平均损失 \[ \mathcal{L_{in}}(h)=\frac{1}{N}\sum_{n=1}^N(h(\mathbf{x}_n)-y_n)^2 \] \(h(\mathbf{x}_n)\)是回归模型的结果

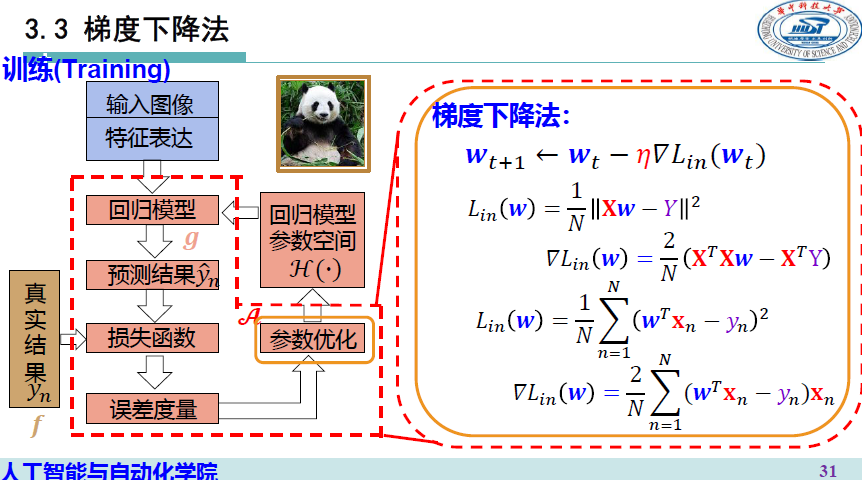
在线性回归模型中，\(\hat{y_n} = h(\mathbf{x}_n) = \mathbf{w}^T \mathbf{x}_n\) \[ \mathcal{L_{in}}(\mathbf{w})=\frac{1}{N}\sum_{n=1}^N(\mathbf{w}^T\mathbf x_n-y_n)^2 \] 则 \[ g=\arg \mathop{\min}\limits_{\mathbf w}\frac{1}{N}\sum_{n=1}^N(\mathbf{w}^T\mathbf x_n-y_n)^2 \]

向量/矩阵形式

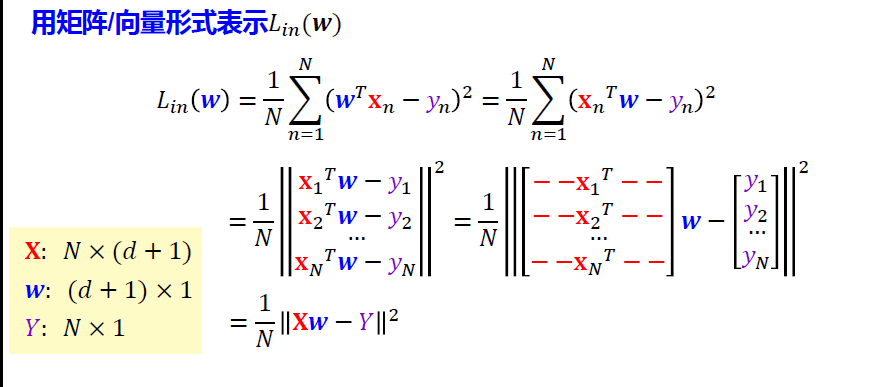
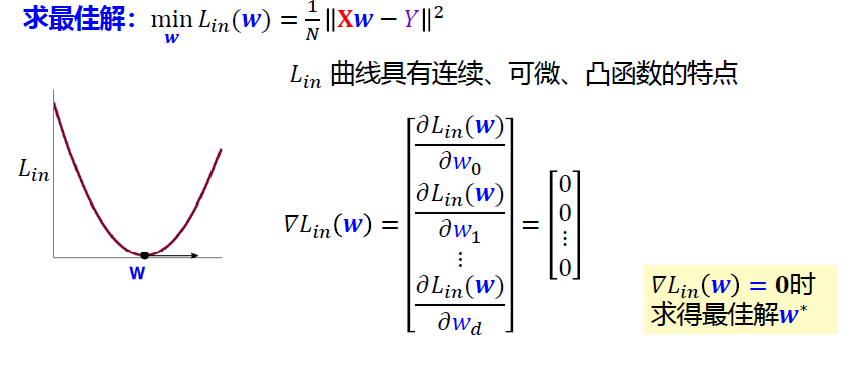
广义逆解法——线性回归的解析解

\(\nabla \mathcal{L}_{in}(\mathbf{w})=0\)时，求得最佳解\(\mathbf w^*\)

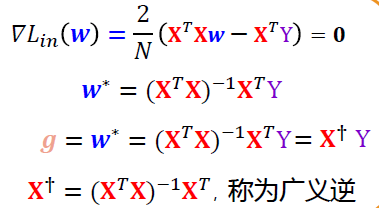
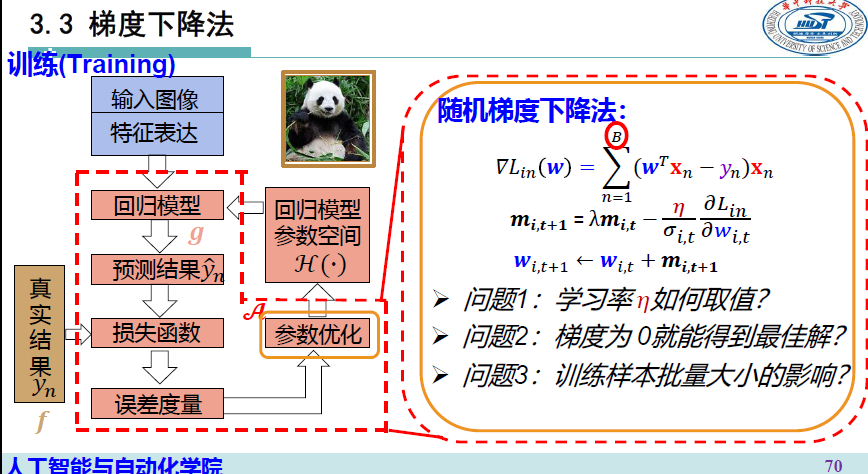
梯度下降法 Gradient Descent

各种 GD算法

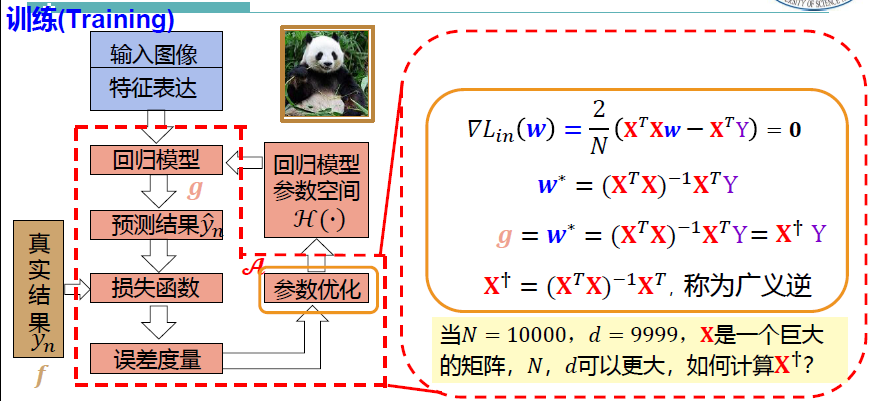
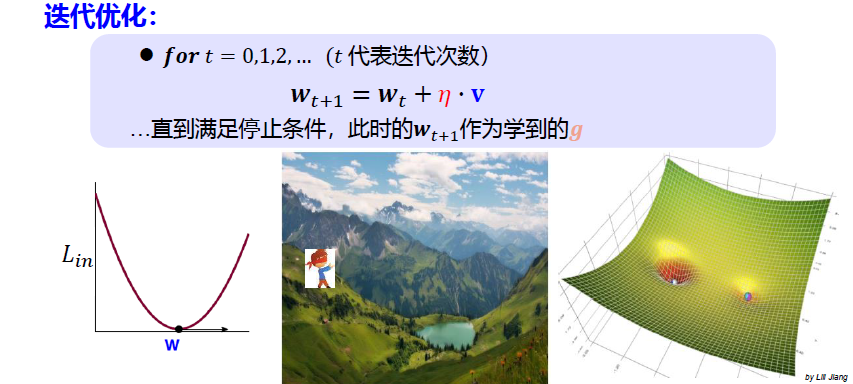
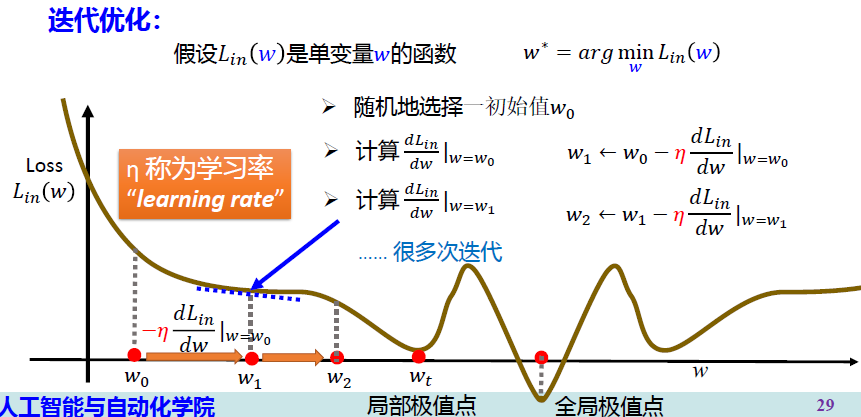
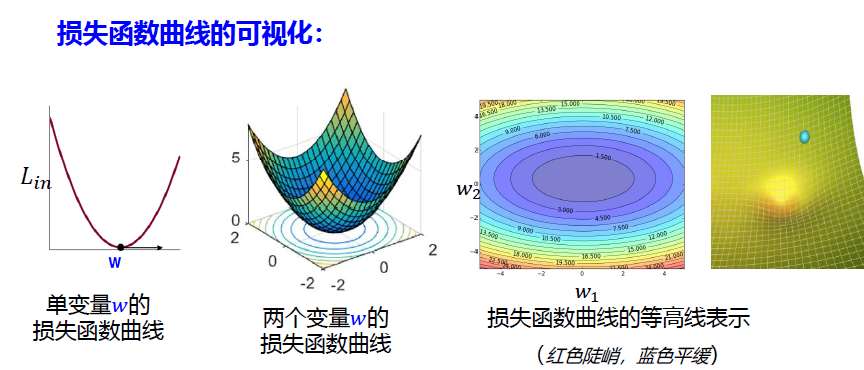
梯度下降法
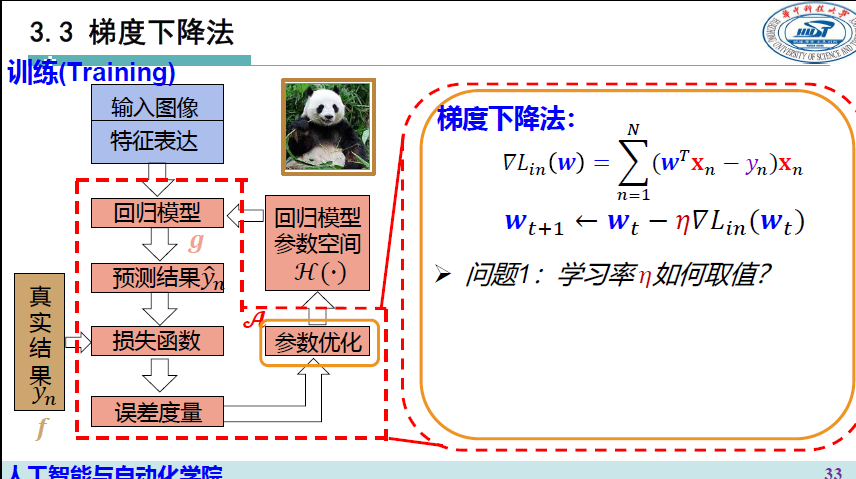
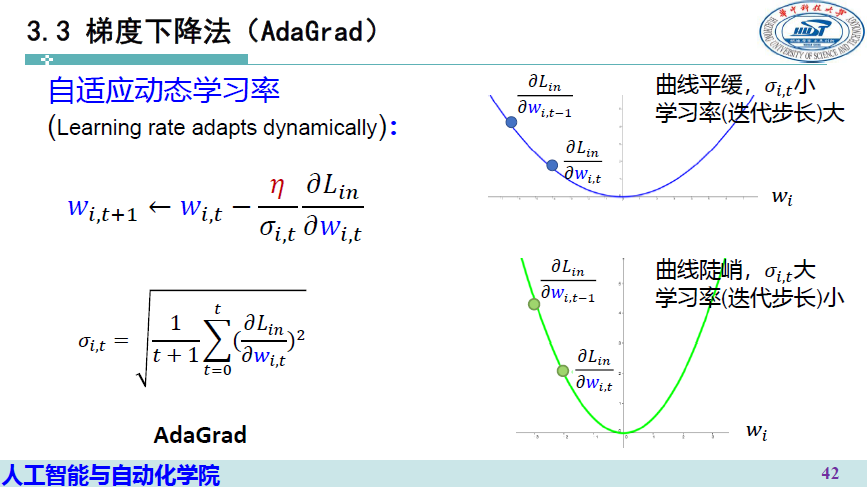
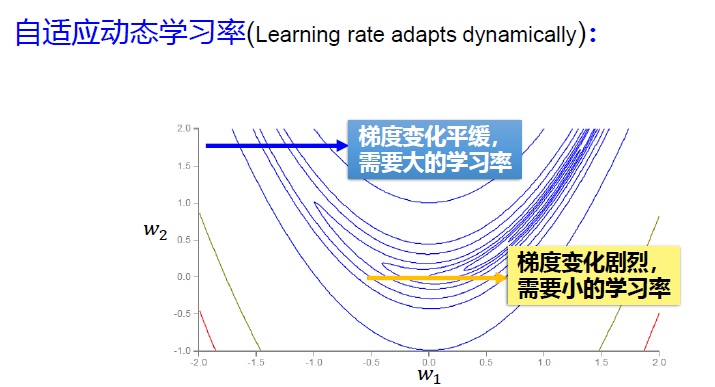
AdaGrad 自适应梯度下降法>
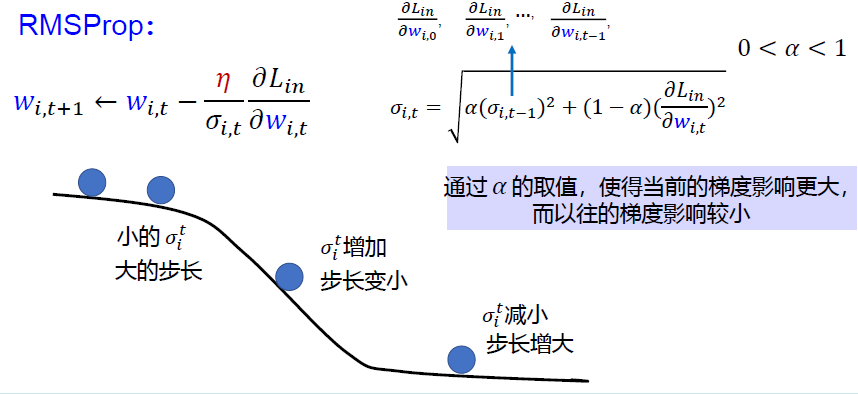
RMSProp

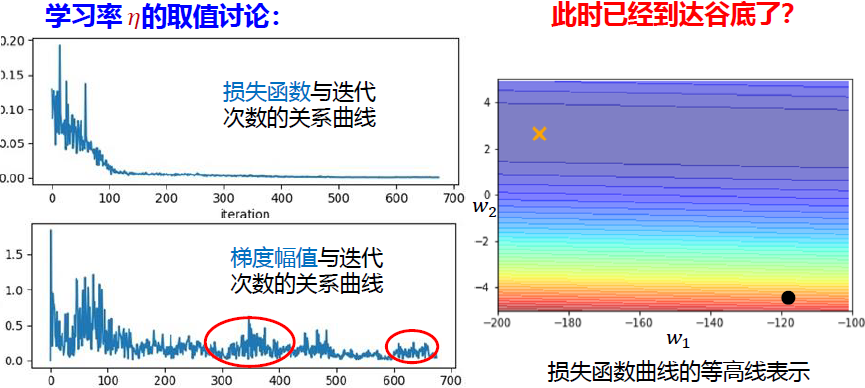
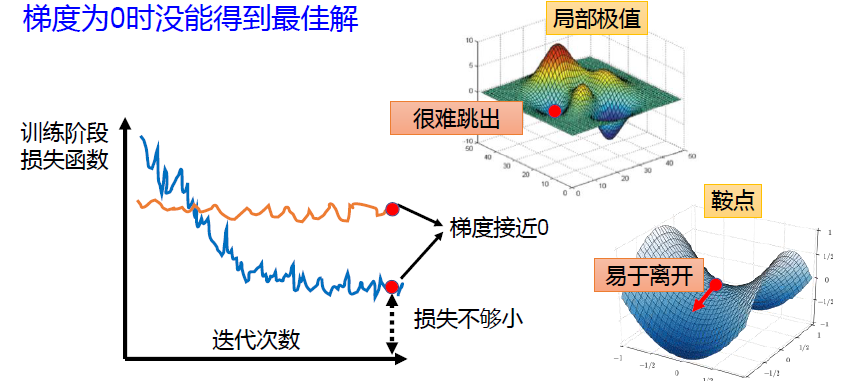
问题2：梯度为0就能得到全局最优解吗？  ×

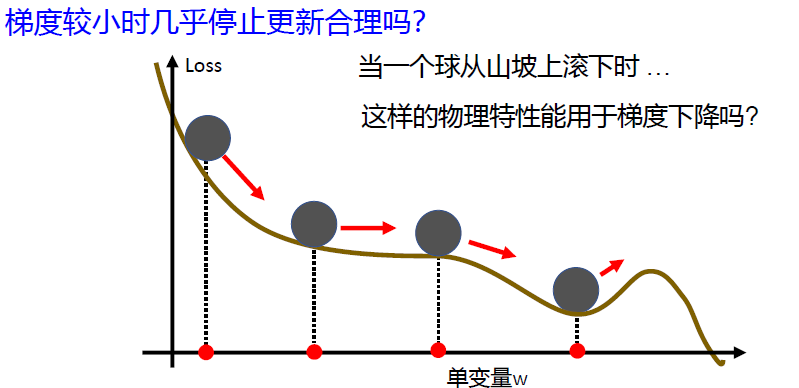
Momentum 动量法梯度下降
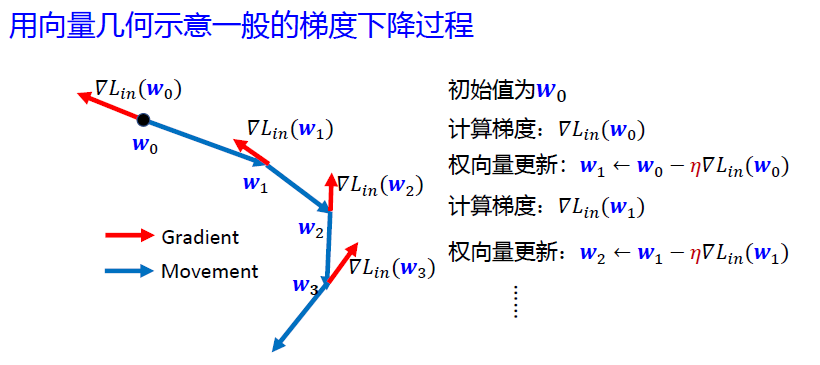
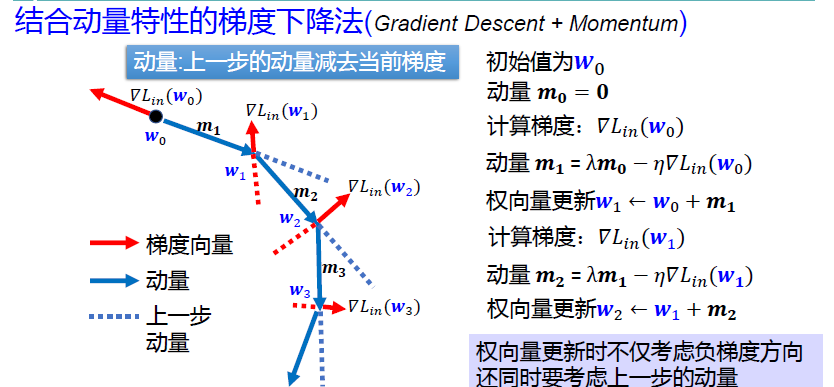
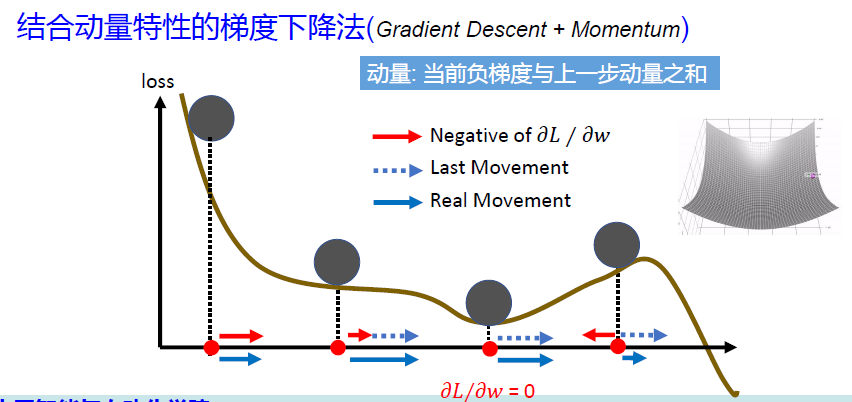
Adam 亚当优化器

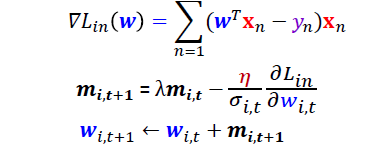
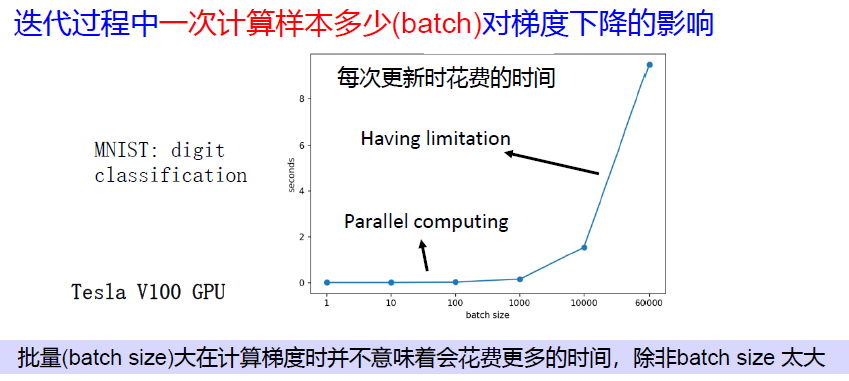
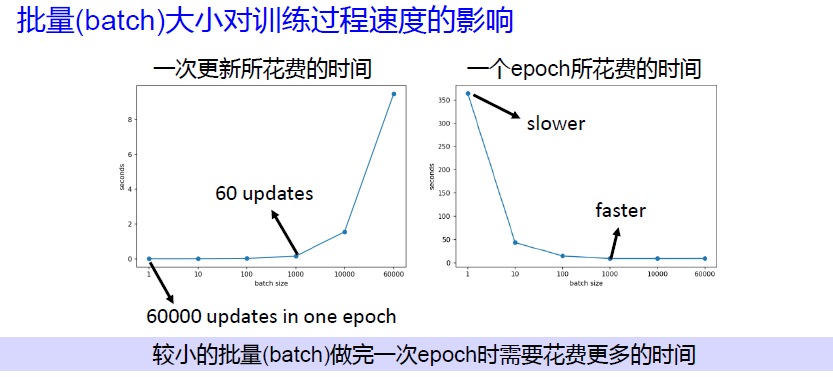
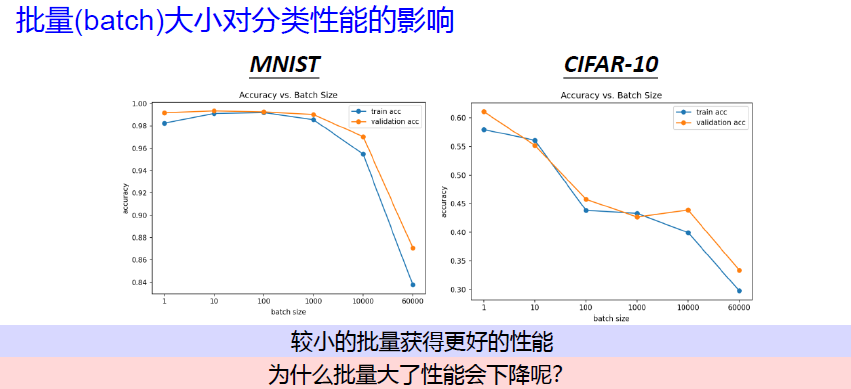
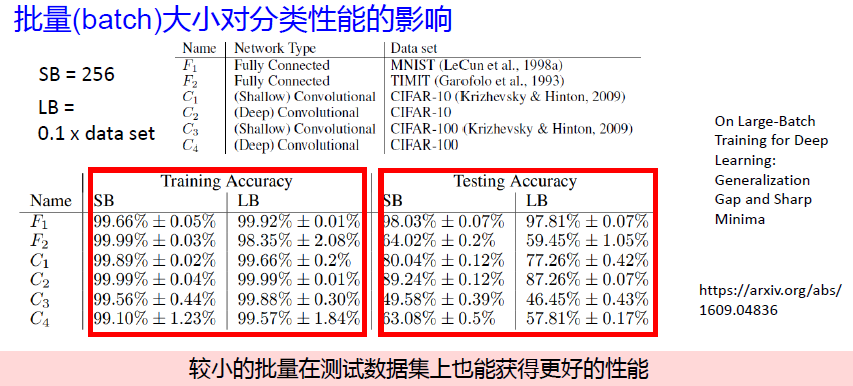
问题3：训练样本批量大小的影响？

batch_size 的影响

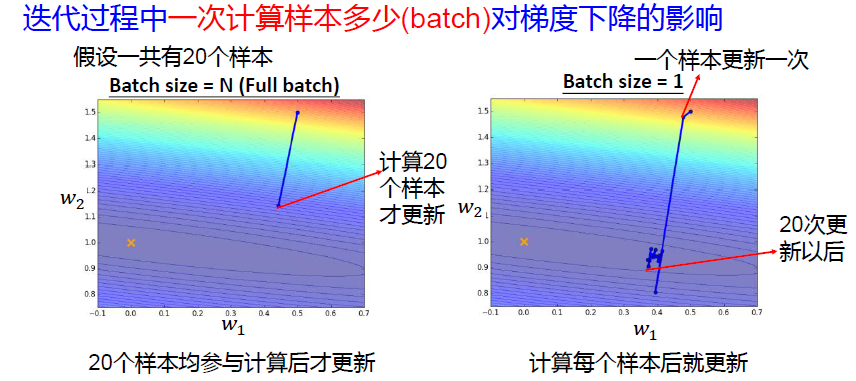
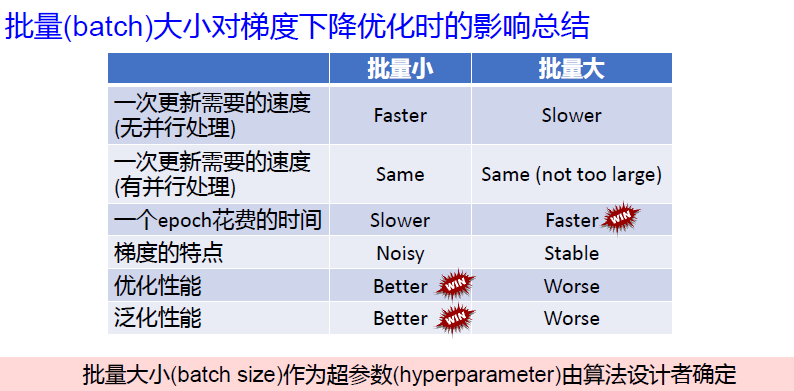
小结

作业

手写作业